Para determinar a forma de objectos o  mais óbvio é olhar para eles, utilizando um microscópio se forem muito pequenos. Mas não se conseguem ver detalhes que sejam menores que o comprimento onda da radiação utilizada para os ver. Se quisermos olhar para moléculas, ou seja, "ver" com resolução atómica  necessitamos  de luz de comprimento onda na gama dos raios-x.

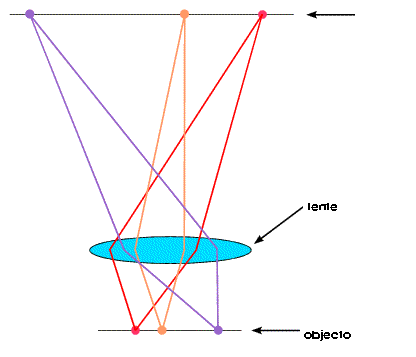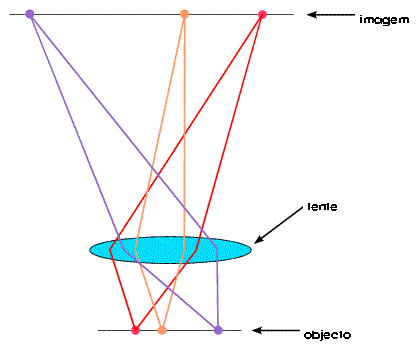
Mas não é possível construir um microscópio de raios-X para olhar para moléculas porque  não existem lentes de raios-X. Podemos no entanto simular uma lente de raios-X num computador!  Num microscópio a luz incide sobre o objecto e é difractada em várias direcções; a lente colecta os raios difractados e reconstitui a imagem. Numa experiência de difracção de raios-X a reconstituição da imagem é feita com o auxílio de programas. A radiação difractada por um objecto é a transformada de Fourier desse objecto ou a imagem desse objecto no espaço de Fourier ou espaço recíproco.  A reconstituição da imagem reside na passagem para o espaço real, o que implica inverter esta transformada de Fourier. A lente simulada no computador consiste num conjunto de programas que calculam a inversa da transformada de Fourier a partir das imagens de difracção obtidas.

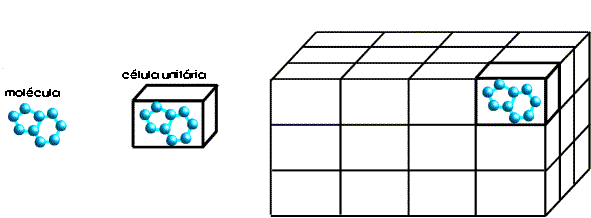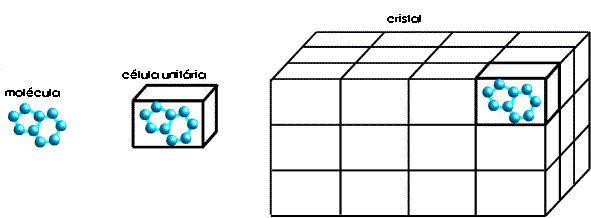
A difracção de raios-X de uma única molécula seria muito fraca e impossível de detectar mesmo no detector mais sensível e sem ruído de fundo. Num cristal existem muitas moléculas com a mesma orientação e se as ondas difractadas estiverem em fase (interferência construtiva) o sinal pode ser detectado. Um cristal actua assim como um amplificador do sinal de uma molécula.
 
 

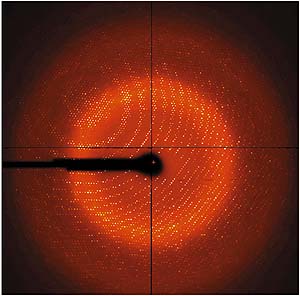
O padrão de difracção de um cristal é assim um conjunto de pontos, correspondentes à intensidade da radiação difractada que chega ao detector. Se pensarmos nos electrões de um átomo numa dada posição na rede cristalina como emissores de ondas, o que é medido no detector depende da interferência dessas ondas, por sua vez dependente da direcção das ondas incidendentes e refractadas e das posições relativas dos átomos. O percurso da radiação desde os átomos ao detector determina o que acontece: se a diferença de percurso da radiação difractada por um electrão for um múltiplo inteiro do comprimento de onda, as ondas difractadas chegam em fase ao detector e as suas amplitudes são somadas; se for metade de um múltiplo inteiro chegam em oposição de fase e as suas amplitudes cancelam.

As condições para a difracção de ondas em fase são dadas pela lei de Bragg.

Pode igualmente verificar-se que a posição dos picos na onda resultante da interferência de dois átomos depende da sua posição relativa. A posição de um pico numa onda é descrita pela sua fase. E esse é o grande problema na determinação da estrutura de um cristal por difracção de raios-X: para calcularmos a função inversa da transformada de Fourier precisamos de saber não só as amplitudes como também as fases das ondas difractadas. O que é possível medir  é apenas a intensidade da radiação que chega ao detector (o quadrado da amplitude); perdemos assim toda a informação sobre a fase das ondas difractadas. É então necessário derivar métodos indirectos para deduzir a informação perdida.