


Now, it's all very well being able to do all this fancy stuff, but if you've only got Boxes, Cones, Spheres, and Cylinders, how far are you going to get? Not very. That's why VRML provides a number of other geometry nodes. You can use these to build up arbitrary or complex shapes to enhance your world. I'm going to cover the basic fields of these nodes, so that you can get going and use them. I'll cover the more complex fields that allow you to change the look of the nodes in the next tutorial. Anyway, we'll start with the most fundamental of these advanced geometry nodes, the IndexedFaceSet.
The IndexedFaceSet node is a collection of faces, which you define manually, and hence build up your own objects of any shape. The basic idea is very simple, as shown in the diagram below:
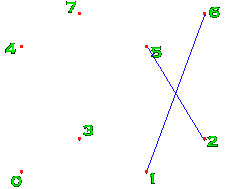
Say you want to define a cube, or part of a cube. You first need to define the eight vertices, numbered 0-7 in the diagram. Then, you need to define the faces. To define the face with the blue cross on it, you would say that it uses the vertices 1, 2, 6 and 5. And that's all there is to it. Do that for each face, and you've done it! One word of warning. If the vertices of a face are not coplanar (i.e. are not all on a flat plane), then the browsers will get confused and the results are undefined. It is best to use triangular faces, with only three points to a face, as then they will always be coplanar. If you want more vertices per face, be very careful. However, you can make up any shape out of triangles, so that's probably the best way to go.
The actual syntax of a basic IndexedFaceSet node is as follows:
IndexedFaceSet {
coord SFNode NULL
coordIndex MFInt32 []
solid SFBool TRUE
}
The coord field contains a Coordinate node, which simply consists of a list of 3D points, as shown in the example below. These are the points that will make up your IndexedFaceSet. The next field is coordIndex. This is the face list. To define a face, you enter the index of each point on it in this list, followed by a -1 to indicate that one face is finished and another can start. The index of the point is it's number in the coordinate list. If you are looking at the face, the index values should be entered in anticlockwise order for the face to be facing you, and not away from you. The only other field is solid. If your object is not fully closed, you need to tell the browser to draw the inside faces, otherwise it won't. So, you can set solid to FALSE in this case. The example below defines a cube with four faces missing, which isn't solid. It is the one seen in the example at the end of the tutorial. There is a lot more you can do with IndexedFaceSets, but these involve using colours and normals, which we haven't got to yet. This will all be covered in the next tutorial.
IndexedFaceSet {
coord Coordinate {
point [ -2 0 2, 2 0 2, 2 0 -2, -2 0 -2
-2 4 2, 2 4 2, 2 4 -2, -2 4 -2]
}
coordIndex [ 0 4 7 3 -1
1 2 6 5 -1
4 5 6 7 -1
2 3 7 6 -1 ]
solid FALSE
}
A very close relative of the IndexedFaceSet is the IndexedLineSet. This node defines a number of lines to be drawn in the world between coordinates. This is useful for just having thin lines, or for making wireframe objects. It's all done in exactly the same way as for the IndexedFaceSet, except that there is no solid field, and the coordIndex field specifies the point indices for each line, with a -1 in between each one.
IndexedLineSet {
coord SFNode NULL
coordIndex MFInt32 []
}
The 'ropes' in the example are done with an IndexedLineSet. The lines are infinitely thin. They are coloured, but not textured, as there is nothing to texture. Lines are not affected by collision detection, so the viewer can walk straight through them.
Again, pretty much identical to IndexedLineSet, PointSet defines a set of points in space. These are drawn at a size determined by the browser, which there is no way to change at present. This node is identical to the previous one, except it has no coordIndex field, as there are no connections between the points. The points are drawn in the same way as lines, and are not affected by collision.
PointSet {
coord SFNode NULL
}
The next two nodes are both specialised and optimised versions of the IndexedFaceSet. The first of these I will cover is the ElevationGrid. In a world, it is common to want to display a ground plane. Now, a flat plane isn't very interesting, so you can use an ElevationGrid instead. This allows you to create a ground plane with variable height. This is done by specifying a number of heights, which are made into a grid. The grid size is specified with xDimension and zDimension fields, and the xSpacing and zSpacing fields. These define the dimensions and spacing between the points in both the X and Z directions. The list of points starts from the one in the far left, proceeding to the near right corner, when looking down the -Z axis. If the solid field is TRUE, the object is not visible from beneath. If you need it to be, set it to FALSE. The basic syntax is shown below.
ElevationGrid {
xDimension SFInt32 0
zDimension SFInt32 0
height MFFloat []
xSpacing SFFloat 0.0
zSpacing SFFloat 0.0
solid SFBool TRUE
}
ElevationGrid {
xDimension 6
zDimension 6
height [1.5, 1, 0.5, 0.5, 1, 1.5,
1, 0.5, 0.25, 0.25, 0.5, 1,
0.5, 0.25, 0, 0, 0.25, 0.5,
0.5, 0.25, 0, 0, 0.25, 0.5,
1, 0.5, 0.25, 0.25, 0.5, 1,
1.5, 1, 0.5, 0.5, 1, 1.5]
xSpacing 5.0
zSpacing 5.0
}
In this example, there are 6 points in both the X and Z directions, and the points are 5 metres apart in both directions. This produces a square grid 25 metres to a side. The values in the height field are the heights at each point. The first is placed at 0,0, and the last will be at +25, +25. This object also has more advanced fields that will be covered next time.
The last of these geometry nodes to cover is the Extrusion. This takes a 2D cross-section and extrudes it along a path, called a spine. You can also alter the scale at each point, shrinking and expanding the cross-section. The syntax is shown below:
Extrusion {
crossSection MFFloat []
beginCap SFBool TRUE
endCap SFBool TRUE
scale MFVec2f []
solid SFBool TRUE
spine MFVec3f []
}
The crossSection field is a list of 2D points, in anticlockwise order, which define the cross-section of the extruded object. This section is extruded along the line defined by the spine field, which is a list of 3D points. At each point in the spine, you can define a scale factor, in the scale field, a list of pairs of float values, one each for the X and Z directions. The solid field is the same as before, and the beginCap and endCap fields define whether the extrusion has a cover over either end. So, this example would extrude a square along a four-point spine with varying scale factors:
Extrusion {
crossSection [1 1, 1 -1, -1 -1, -1 1, 1 1]
spine [0 0 0, 0 2 0, 1 3 0, 2 3 0]
scale [1 1, 1 0.5, 0.5 1, 0.5 0.5]
}
You can see what this extrusion actually looks like up close in this example and the associated code. One important thing to remember with extrusions is that, when creating the cross-section, you need to repeat the starting point at the end if you want it to be closed.
You can see the effects of all this stuff by taking a look at the example world. The 'tent' is an IndexedFaceSet, the 'ropes'
are an IndexedLineSet, the ground is an ElevationGrid and the 'thing' is an Extrusion. There's no PointSet, as
I couldn't think of a decent use for it. Still, you don't really need an example for that, it's so simple. Anyway, take a look at the example
for this tutorial:
Tutorial 10 World
and code.
Right. That's the basics of these advanced objects. Next tutorial I'll cover normals, colors and so on to make these objects look better.


