Resol old

II.1

1.

Considere uma orbital 2p_Z no modelo do átomo da mecânica ondulatória. Como sabe, de acordo com este modelo, o electrão que ocupa a orbital 2p_Z não se manifesta no plano XY. Qual das seguintes observações é verdadeira?

A

Neste modelo o electrão é descrito por uma onda progressiva. A função de onda que descreve o electrão na 2p_Z começa no núcleo e dirige-se para um dos lados do plano XY.

B

Neste modelo o electrão é descrito por uma onda estacionária. A função de onda que descreve o electrão na 2p_Z tem um plano nodal XY. O electrão manifesta-se apenas de um dos lados deste plano.

C

Neste modelo o electrão é descrito por uma onda estacionária. A função de onda que descreve o electrão na 2p_Z tem um plano nodal XY. O electrão manifesta-se igualmente acima e abaixo deste plano.

D

O electrão não passa da zona de Z positivo (acima do plano XY) para a de Z negativo (abaixo do plano XY), nem vice versa. Por isso nunca se manifesta em XY.

E

O electrão passa da zona de Z positivo (acima do plano XY) para a de Z negativo (abaixo do plano XY), e vice versa. Mas esta passagem faz-se através do núcleo, por isso não é observado no plano XY.

Resposta correcta: C - O electrão manifesta-se igualmente acima e abaixo do plano XY

III.1

A primeira energia de ionização de um átomo de flúor é inferior à de um átomo de néon (E_i1(F) = 17.4 eV e E_i1(Ne) = 21.6 eV). Dê uma explicação quantitativa.

A energia de ionização é proporcional a Z_ef²/n².

1) Tanto no F como no Ne o número quântico principal, n, do electrão que sai (ionizado) é o mesmo, n = 2

2) Z_ef (2p, Ne) = Z_ef (2p, F) + 0.65 (o electrão 2p do Ne não blinda completamente o protão do núcleo), logo E_i1(Ne) > E_i1(F)

Com o anterior (ou equivalente) a resposta ficaria completa, mas poderiam acrescentar:
F 1s² / 2s² 2p⁵ / Z_ef (2p, F) = 9 – (2 ´ 0.85 + 6 ´ 0.35) = 5.20
Ne 1s² / 2s² 2p⁶ / Z_ef (2p, Ne) = 10 – (2 ´ 0.85 + 7 ´ 0.35) = 5.85

III.2

Explique os valores experimentais das energias de ionização do azoto (N) e do oxigénio (O) que encontra na Tabela Periódica.

A energia de ionização é proporcional à razão (Z_ef /n)² para o electrão em causa.

EI(N) = 14.5 eV
EI(O) = 13.6 eV

Configuração electrónica do azoto: (1s² )(2s² 2p³)

Z_ef (2p, N) = 7 - (4x0.35 + 2x0.85) = 3.9

Configuração electrónica do oxigénio: (1s² )(2s² 2p⁴)

Z_ef (2p, O) = 8 - (5x0.35 + 2x0.85) = 4.55

(Z_ef /n)² (2p, N) = (3.9/2)²= 3.8

(Z_ef /n)² (2p, O) = 5.2

A energia de ionização do oxigénio deveria ser superior à energia de ionização do azoto, uma vez que a razão (Z_ef /n)² é maior para o electrão 2p do oxigénio. Experimentalmente verifica-se que a energia de ionização do azoto é superior porque as regras de Slater não contemplam o grau de preenchimento das orbitais, isto é, não consideram a repulsão interelectrónica. No azoto o electrão é removido de uma orbital semipreenchida enquanto no oxigénio o electrão é removido de uma orbital completamente preenchida.

III.3

A afinidade electrónica do azoto (E_A(N) = -7 kJ/mol) é muito inferior à do carbono (E_A(C) = 122 kJ/mol).

a) Diga de que variáveis depende a afinidade electrónica e mostre, quantitativamente, que era esperada uma variação no sentido oposto.

b) Explique porque é que o cálculo não prevê correctamente os valores relativos de E_A.

a) E_A(X) = E_I(X^-) que é proporcional a Z_ef² ⁄ n² (calculado em relação ao electrão exterior de X^-).
⁷N^- 1s²2s² 2p⁴ ⁶C^- 1s²2s² 2p³
O número quântico principal do electrão que sai é idêntico nos dois casos n=2
Z_ef (2p, N^-) = 7 – (5x0.35 + 2x0.85) = 3.55 > Z_ef (2p, C^-) = 6 – (4x0.35 + 2x0.85) = 2.90
logo deveria ser E_I(C^-) < E_I(N^-) e E_A(C) < E_A(N)

b) No N o electrão vai entrar numa orbital 2p já com um electrão que o vai repelir, o que não acontece no C. As regras de Slater não contabilizam este efeito.

III.4

Explique quantitativamente a seguinte afirmação: O neon tem uma energia de ionização elevada e uma electroafinidade baixa.

IV.1

1. Desenhe o diagrama de energias para as orbitais moleculares da espécie diatómica ClF indicando: i) as energias de ionização dos átomos constituintes e da molécula, ii) os tipos de orbitais moleculares (s , p , etc.) envolvidas, iii) a ordem de ligação, iv) as propriedades magnéticas que prevê para a molécula.
NOTA: Indique no diagrama apenas as Orbitais de Valência

i) Ei indicadas no diagrama

ii) Tipos de OM indicados no diagrama

iii) OL = (8 – 6)/2 = 1 Cl–F

iv) Diamagnética porque não tem electrões desemparelhados

2. Faça uma estimativa quantitativa do momento dipolar da molécula.

momento dipolar (m_ClF) = q ´ d = %CI/100 ´ e (carga do electrão) ´ d_ClF
electronegatividade (Cl) = 3.16
electronegatividade (F) = 3.98
diferença de electronegatividades = 0.82, a que corresponde uma percentagem de carácter iónico %CI= 15% (lida na Tabela Periódica)

d_ClF = r_cov(Cl) + r_cov(F) = 99 pm + 72 pm = 171 ´ 10^–12 m

m_ClF = 0.15 ´ 1.6 ´ 10^–19 C ´ 171 ´ 10^–12 m = 4.10 ´ 10^–30 C m = 1.2 D

IV.2

1. Desenhe o diagrama de energias das orbitais moleculares do monóxido de azoto (NO), identificando no mesmo diagrama as energias de ionização dos átomos constituintes e os tipos de orbitais moleculares (s, p, etc.) envolvidas. Determine a ordem de ligação no NO e preveja as propriedades magnéticas da molécula.

2. Utilizando os dados da Tabela Periódica faça uma estimativa do momento dipolar da molécula HF.

1. Molécula NO

EI(N) = 14.5 eV
EI(O) = 13.6 eV

Configuração electrónica do azoto: 1s² 2s² 2p³
Configuração electrónica do oxigénio: 1s² 2s² 2p⁴

Diagrama de energia das orbitais moleculares

Uma vez que a energia de ionização do N é maior que a energia de ionização do O as orbitais 2p do azoto têm menor energia. Representando apenas as orbitais de valência de ambos os átomos tem-se:

As orbitais atómicas sigma 1s não coalescem significativamente. Ficam, portanto, como orbitais não ligantes.

NOTA: Nesta molécula as orbitais sigma 2p e pi 2p ligantes, são quase isoenergéticas (é a última molécula em que se observam os efeitos da inversão sigma-pi). Porém, tal como indicado nas aulas, não se espera que o aluno tenha em conta a inversão sigma-pi.

OL = (nº de electrões ligantes - nº de electrões antiligantes)/2= (8 -3 )/2 = 2.5
A molécula é paramagnética.

2. Molécula HF

momento dipolar (m_HF) = q x d = %CI/100 x e (carga do electrão) x d_HF

electronegatividade do H=2.2
electronegatividade do F=3.98

diferença de electronegatividades = 1.78, a que corresponde uma percentagem de carácter iónico %CI= 55% (lido na Tabela Periódica)
d_HF = r_cov(H) + r_cov (F) = (30 + 72) x10^-12 m = 102 x10^-12m

m_HF = 0.55 x 1.6x10^-19C x 102 x10^-12 m = 8.976 x10^-30 C m = 2.7 D

IV.3

1. Desenhe o diagrama de orbitais moleculares do ião N₂⁺, identificando no mesmo diagrama as energias de ionização dos átomos constituintes e os tipos de orbitais moleculares (s, p, etc.) envolvidas. Determine a ordem de ligação nesta espécie e preveja as propriedades magnéticas da molécula.

2. Utilizando os dados da Tabela Periódica faça uma estimativa do momento dipolar da molécula LiH.

Dados e constantes de conversão:

h (constante de Planck) = 6.62618 x 10^-34 J s
e (carga do electrão) =1.60x10^-19 C
1 electrão-volt (eV) = 1.60 x 10^-19 C m
1 Debye (D) = 3.33 x 10^-30 C m

V.1

Considere as seguintes moléculas:
A HOCH CH₂, álcool vinílico
B HOOC CH CH COOH, ácido trans-butenodióico
1. Descreva pela teoria do Enlace de Valência a estrutura molecular de cada uma, indicando: (i) hibridações e configuração electrónica dos átomos no estado hibridado; (ii) ângulos de ligação; (iii) tipos de ligação; (iv) pares de electrões não partilhados; (v) existência e número de orbitais p deslocalizadas.

Molécula A

(i) C1 e C2 1s² sp₂¹ sp₂¹ sp₂¹ 2p_z¹
O 1s² sp₃² sp₃² sp₃¹ sp₃¹
(ii) ver figura
(iii) ver figura
(iv) 2 pares sp₃ no O
(v) não tem

Molécula B

(i) C1 e C2    1s² sp₂¹ sp₂¹ sp₂¹ 2p_z¹ ângulos de 120º
O1    1s² sp₂² sp₂² sp₂¹ 2p_z¹ ângulos de 120º
O2    1s² sp₃² sp₃² sp₃¹ sp₃¹ ângulos de 109º
(ii) ver figura
(iii) ver figura
(iv) 8 pares nos O
(v) 6 orbitais p deslocalizadas

2. Represente a estrutura da unidade repetitiva ou de um pedaço de cadeia do polímero formado a partir da molécula A.

3. Descreva as forças intermoleculares mais importantes neste polímero.

Keesom (o mero é polar), Debye (pouco importantes), London e ligações por Pontes de Hidrogénio.

V.2

Diga, justificando, qual das substâncias: diclorometano, CH₂Cl₂, ou dimetilamina, (CH₃)₂ NH, dissolve melhor a trimetilamina, (CH₃)₃ N.
Identifique numa tabela todas as interacções moleculares.

Estrutura, dipolos moleculares e pares de electrões isolados.

	nº electrões	Keesom	Debye	London	Pontes H
(CH₃)₃ N	34	+	(+)	+++	N
CH₂Cl₂	42	+	(+)	++++	N
(CH₃)₃ N + CH₂Cl₂		+	(+)	+++	N

(CH₃)₃ N	34	+	(+)	+++	N
(CH₃)₂ NH	26	+	(+)	++	+++
(CH₃)₃ N + (CH₃)₂ NH		+	(+)	++	+++

Ambos os solventes devem dissolver bem a trimetilamina porque não há perda significativa de energia das ligações intermoleculares em nenhum dos casos. A formação de ligações de hidrogénio entre a dimetil e trimetilamina e a perda de ligações de London no caso do diclorometano pode indicar uma maior solubilidade na dimetilamina.

V.3

1. Descreva a estrutura molecular do acrilonitrilo, CH₂CHCN, indicando: (i) ângulos de ligação aproximados, (ii) tipos de ligação (s, p) (iii) configuração electrónica dos átomos hibridados, (iv) pares de electrões isolados e, (v) se existirem, o número de orbitais deslocalizadas e de electrões que as ocupam.

Ligações na molécula

Estrutura da molécula

(i), (ii), (iv) indicados na figura
(iii) Hibridações
C₁ e C₂ 1s² 2sp₂¹ 2sp₂¹ 2sp₂¹ 2p_z¹
C₃ 1s² 2sp¹ 2sp¹ 2p_y¹ 2p_z¹N 1s² 2sp² 2sp¹ 2p_y¹ 2p_z¹o único par isolado da molécula é 2sp² do N
(v) as orbitais 2pz dos C e do N formam um sistema p deslocalizado constituído por 4 orbitais. 2 ligantes preenchidas com os 4 electrões disponíveis e 2 antiligantes vazias.

2. O acrilonitrilo dá origem a um polímero de fórmula - (CH₂CHCN)-_n.

i) Classifique este polímero

Homopolímero de adição

ii) Quais as interacções que se estabelecem entre as cadeias deste polímero?

Os meros são polares, logo haverá interacções de Keesom, Debye e London. Não há ligações por pontes de H.

V.4

Discuta detalhadamente a miscibilidade do acrilonitrilo (P.E. = 77ºC) em metanol, CH₃OH (P.E. = 65ºC).

São ambas moléculas polares.
A plolarizabilidade será proporcional ao nº de electrões: o CH₂CHCN tem 28 e o CH₃OH tem 18 electrões.
Têm pontos de ebulição semelhantes logo a energia das interacções moleculares deve ser semelhante (um pouco maior no acrilonitrilo).

Keesom Debye London Pontes H

CH₂CHCN + (+) +++ --------

CH₃OH ++ (+) + ++

CH₂CHCN + CH₃OH + (+) ++ ++

A mistura dos dois líquidos deve ser favorável. A energia da interacção é semelhante (DHº_mist aprox 0) e a entropia de mistura positiva (DSº_mist > 0).

V.5

1. Descreva a estrutura molecular do ceteno (etenona), CH₂CO, indicando (i) ângulos de ligação aproximados, (ii) tipos de ligação (iii) hibridações dos átomos (iv) e, se existirem, o número de orbitais deslocalizadas e de electrões que as ocupam.

2. O PVC é obtido por polimerização do cloreto de vinilo CH2CHCl.

i) Escreva a unidade repetitiva deste polímero e classifique-o.

ii) Quais as interacções que se estabelecem entre as cadeias deste polímero?

V.6

Discuta detalhadamente a miscibilidade do diclorometano CH₂Cl₂ (P.E. = 40ºC) em água, H₂O, (P.E. = 100ºC).

V.7

No H₃P o ângulo HPH é de 93º 30’ e no amoníaco, H₃N o ângulo HNH é de 107º. Qual a afirmação verdadeira?
c	O azoto não tem orbitais com electrões adequadas para fazer duas ligações com o hidrogénio sem hibridar e o fósforo tem.
c	Ambos os átomos hibridam. O ângulo no caso do azoto é maior devido às repulsões par partilhado – par isolado.
c	Não é necessário invocar hibridação em qualquer dos casos. Os ângulos são diferentes porque as repulsões electrónicas entre orbitais p são maiores no azoto.
c	A molécula de H₃P não é estável mas a de H₃N é. A instabilidade do H₃P resulta do menor ângulo entre os átomos.^.
c	O azoto hibrida em sp₃ para minimizar as repulsões electrónicas e o fósforo não hibrida porque, sendo um átomo maior, as repulsões são menores.

V.8

Descreva a estrutura molecular do composto, CHONCH₂, indicando:
(i) ângulos de ligação aproximados,
(ii) tipos de ligação (s, p)
(iii) configuração electrónica dos átomos hibridados,
(iv) pares de electrões isolados,
(v) se existirem, o número de orbitais deslocalizadas e de electrões que as ocupam.

V.9

Discuta a miscibilidade do O2 em água (T.E. = 100º C) e diclorometano, CH2Cl2 (T.E. = 60º C). Faça-o de acordo com os seguintes passos:
(i) represente a geometria das moléculas e indique os seus momentos dipolares,
(ii) represente num quadro as forças intermoleculares relevantes,
(iii) compare e conclua.

VI/VII.1

Considere uma liga de ouro com 10% (percentagem atómica) em platina
(i) Indique o tipo de liga que se forma

Solução sólida de substituição (átomos de raio semelhante e electronegatividades semelhantes).

(ii) Considerando que o Au cristaliza numa estrutura CFC e tem um raio metálico de 1.79 Å, calcule a massa volúmica desta liga

A massa volúmica será:

r = (massa dos átomos numa célula base) / (volume da célula base)

Volume da célula base
Na estrutura CFC os átomos tocam-se segundo a diagonal da face do cubo, d.
Supondo que a Pt não deforma a estrutura, d = aÖ2 = 4 r(Au) = 7.16´10^-8 cm
A aresta da célula base será a = 5.06´10^-8 cm
E o volume da célula base V(cb) = a³ = 1.295´10^-22 cm³

Massa dos átomos numa célula base
Numa célula base há (6´1/2 + 8´1/8 =) 4 átomos, 0.90´4 de Au e 0.10´4 de Pt
MA(Au) = 196.97 g/mol, ma(Au) = MA/N_A = 3.27´10^-22 g/átomo
MA(Pt) = 195.09 g/mol, ma(Pt) = MA/N_A = 3.24´10^-22 g/átomo
A massa da célula base será: M(cb) = 0.90´4´ma(Au) + 0.10´4´ma(Pt) = 1.307´10^-21 g

Logo a massa volúmica será 10.1 g/cm³.

VI/VII.2

1. Em cada par de compostos a seguir indicados seleccione o de maior dureza. Justifique.
i) NaF e KCl
ii) KCl e CaCl₂

Em princípio, o de maior dureza será o que tiver maior |U| (energia de rede).
Admitimos que as diferenças entre as constante de Madelung, A, e os expoentes de Max Born, n, não afectam as conclusões
|U| µ Z_catião ´ Z_anião / r₀

i) Z_catião ´ Z_anião(NaF) = Z_catião ´ Z_anião(KCl) = 1 ; r₀(NaF) < r₀(KCl). Logo dureza(NaF) > dureza(KCl).
ii) Z_catião ´ Z_anião(KCl) = 1, Z_catião ´ Z_anião(CaCl₂) = 2 ; r₀(KCl) > r₀(CaCl₂). Logo dureza(CaCl₂) > dureza(KCl).

2. Em cada par de substâncias a seguir indicadas indique a de maior temperatura de fusão. Justifique.
i) Na e Al

São ambos metais. A energia de coesão e (temperatura de fusão) será tanto maior quanto maior for o grau de preenchimento dos níveis ligantes.

N átomos de Na : banda de Bloch com 4N níveis (3s+3p), com N electrões, 0.5N níveis preenchidos.
N átomos de Al : banda de Bloch com 4N níveis (3s+3p), com 3N electrões, 1.5N níveis preenchidos.

TF(Al) > TF(Na)

ii) CO₂ e C_diamante

CO₂ : composto molecular (interacções de London)
C_diamante: cristal covalente (energia de ligação pelo menos uma ordem de grandeza superior à das interacções moleculares)

TF(C_diamante) >> TF(CO₂)

VI/VII.3

Considere as seguintes substâncias: potássio (K), cloreto de potássio (KCl), hidreto de potássio (KH), crómio (Cr) e germânio (Ge).

1. Classifique-as, justificando a sua resposta, do ponto de vista da natureza da ligação química.

K e Cr metais: átomos idênticos de electronegatividade muito baixa. Bandas de valência e de condução sobrepostas. Ligação deslocalizada.

KCl e KH cristais iónicos: grande diferença de electronegatividades (ci(KCl) = 74%, ci(KH) = 39%). No caso do KH a % de carácter covalente é elevada mas em qualquer deles o "gap" entre as orbitais ligantes (banda de condução) e antiligantes (banda de valência) é elevado. Ligações localizadas.

Ge Semicondutor: metal (metaloide) de elevada electronegatividade. As bandas de condução e valência estão afastadas embora o "gap" seja pequeno. Ligações deslocalizadas.

2. Esboce o diagrama de bandas do crómio (Cr), explicitando o número de níveis de energia por átomo e o grau de preenchimento da banda. Justifique o facto de este ser um dos elementos do 4º período da TP com maior temperatura de fusão.

Cr [Ar] 3d⁵ 4s¹ 4p⁰

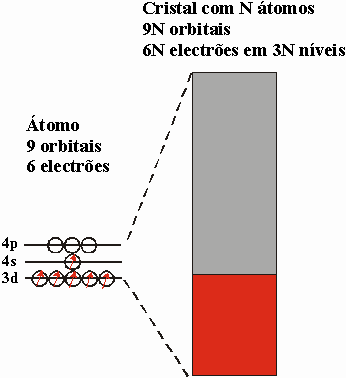
Tem 1/3 da banda preenchida
Logo os níveis ligantes estão preenchidos (cerca de 1/3 da banda). Donde a elevada energia de coesão e ponto de fusão.

3. Calcule a densidade do KCl (estrutura tipo cloreto de sódio) r(K⁺) = 133 pm, r(Cl^- ) = 181 pm.

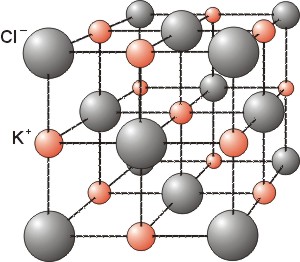
A massa volúmica do KCL será:

r = (massa dos iões numa célula base) / (volume da célula base)

Nesta estrutura o catião tem coordenação octaédrica.
A aresta da célula base será a = 2 r(K⁺) + 2 r(Cl^-) = 6.28´10^-8 cm
Podemos confirmar que os aniões não se tocam pois a diagonal da face d = aÖ2 = 8.88´10^-8 cm > 4 r(Cl^-) = 7.24´10^-8 cm
O volume da célula base será V (cb) = a³ = 2.48´10^-22 cm³

Numa célula base há (6´1/2 + 8´1/8 =) 4 aniões e (1 + 12´1/4 =) 4 catiões
MA(K) = 39.09 g/mol, ma(K) = MA/N_A = 6.49´10^-23 g/átomo
MA(Cl) = 35.45 g/mol, ma(Cl) = MA/N_A = 5.89´10^-23 g/átomo
A massa da célula base será: M(cb) = 4.95´10^-22 g

Logo a massa volúmica será 2.00 g/cm³ e a densidade calculada 2.00.

VI/VII.4

1. Esboce o diagrama de bandas de energia do óxido de magnésio (MgO) e do titânio (Ti) e indique o grau de preenchimento das mesmas.

2. Calcule a densidade de um aço com 0,1% (percentagem atómica) de carbono.

3. Ordene por ordem crescente de dureza as seguintes substâncias, justificando em detalhe a sua resposta.

i) Titânio (Ti) e cálcio (Ca)

ii) Fluoreto de cálcio (NaF), óxido de magnésio (MgO) e óxido de bário (BaO).

VI.5

O ponto de fusão do zinco (Z=30) é 420º C e o do cobre (Z=29) 1085º C. A razão para esta diferença é:
c	66.7% da banda de Bloch do zinco estão preenchidos enquanto que só 61.1% da do cobre está preenchida. Logo, o zinco tem mais electrões em níveis antiligantes e a energia de coesão será menor para este elemento.
c	A banda de Bloch de ambos possui 6N níveis (orbitais cristalinas), mas o cobre tem mais orbitais ligantes preenchidas.
c	66.7% da banda de Bloch do zinco estão preenchidos enquanto que só 61.1% da do cobre está preenchida. Logo, o zinco tem menos electrões em níveis antiligantes e a energia de coesão será menor para este elemento.
c	A energia de coesão depende da energia reticular, U, que é superior no zinco devido ao menor raio.
c	Quanto mais electrões os metais têm, menor o seu ponto de fusão (a coesão diminui ao longo de um período). Como o zinco tem mais electrões, terá menor energia de coesão do que o cobre.

VI/VII.6

Justifique as seguintes observações.

i) O titânio (Ti) tem maior dureza do que o cálcio (Ca).

ii) O óxido de magnésio (MgO) tem maior dureza do que o óxido de bário (BaO).

VIII/IX.1

Calcule a massa de hidróxido de magnésio, Mg(OH)₂ que pode dissolver, a 25 ºC, sem precipitação, em 1000 ml de água e calcule a energia livre de Gibbs padrão (D G⁰) desta reacção a 25 ºC.

Mg(OH)₂ « Mg²⁺ + 2OH^–
K_S(Mg(OH)₂;25ºC) = [Mg²⁺][OH^–]² = S ´ (2S)² = 7.1´ 10^-12
S = 1.21´ 10^–4 M,
massa dissolvida por litro = S ´ MM(Mg(OH)₂) = 1.21´ 10^–4 M ´ 58.3 g/mol = 7.05 mg/1000 ml

DG⁰ (25º C) = – RT ln K = – 8.314 J K^-1 mol^-1 298 K ln(7.1´ 10^-12) = + 6.36´ 10⁴ J mol^-1O valor positivo indica uma maior energia livre de Gibbs dos produtos em relação aos reagentes, o que está de acordo com a baixa solubilidade do Mg(OH)₂.

VIII/IX.2

O produto de solubilidade do carbonato de bário (BaCO₃) a 25 ºC é , a 25 ºC, K_S(BaCO₃;25ºC) = 0.2´ 10^–3 .

1. Considere duas soluções A e B em que as concentrações iniciais de Ba²⁺ e CO₃^2– são respectivamente:
A [0.5´ 10^–3 M (Ba²⁺) e 10^–2 M (CO₃^2–)]
B [0.5´ 10^–2 M (Ba²⁺) e 10^–1 M (CO₃^2–)]
Diga, justificando, em qual das soluções haverá formação de BaCO₃ precipitado.

Q_S = [Ba²⁺][ CO₃^2–]
Q_S (A) = 0.5´ 10^–3 ´ 10^–2 = 0.5´ 10^–5 < K_S
Q_S (B) = 0.5´ 10^–2 ´ 10^–2 = 0.5´ 10^–1 > K_SLogo, na solução B haverá formação de precipitado.

2. Calcule a variação de entalpia padrão, DHº, do processo de dissolução do BaCO₃ e comente o efeito da temperatura na solubilidade deste sal (Princípio de Le Chatelier).

Aplicando a Lei de Hess: DHº_diss = (– 537.6 – 677.14) – (–1219) = + 4.3 kJ mol^-1

A dissolução é endoentálpica (endotérmica a p = cte). Logo, quando a temperatura aumenta o equilíbrio vai evoluir no sentido directo de forma a consumir calor. A solubilidade aumenta com a temperatura.

VIII/IX.3

Considere a pilha electroquímica a seguir esquematizada:

Fe_(s)½Fe²⁺ (10^–4 M) ½ ½ Sn²⁺ (10^–3 M)½ Sn_(s)

a) Calcule a força electromotriz, fem, da pilha a 25 C.
fem = E_dir – E_esq
= Eº_Sn2+/Sn – 0.059/2 ´ log (1/[Sn²⁺]) – {Eº_Fe2+/Fe – 0.059/2 ´ log (1/[Fe²⁺])}
= – 0.163 – 0.059/2 ´ log (10³) – {– 0.440 – 0.059/2 ´ log (10⁴)}
= + 0.306 V

b) Identifique o cátodo e o ânodo, escreva as reacções parciais de eléctrodo e a reacção global da pilha.
Cátodo: Sn Sn²⁺ + 2e ® Sn
Ânodo: Fe Fe ® Fe²⁺ + 2e
Reacção global: Fe + Sn²⁺ ® Fe²⁺ + Sn

c) Calcule a constante de equilíbrio da reacção global da pilha.
1º método
Em equilíbrio E_dir = E_esqEº_Sn2+/Sn – 0.0591/2 ´ log (1/[Sn²⁺]_eq) = Eº_Fe2+/Fe – 0.0591/2 ´ log (1/[Fe²⁺]_eq)
Eº_Sn2+/Sn – Eº_Fe2+/Fe = 0.0591/2 ´ log ([Fe²⁺]_eq /[Sn²⁺]_eq) = 0.0591/2 ´ log (K)
K = 10^9.37 = 2.36´ 10⁹

2º método
DGº = – nFDEº = – RT
ln K = nFDEº/RT
K = exp[2 ´ 96480 (– 0.163 + 0.440)/(8.314 ´ 298)]
K = 2.34´ 10⁹

VIII/IX.4

Sabendo que a força electromotriz da célula galvânica seguinte é f.e.m.= - 0.47 V, a 25 C,

Pt½ H₂(g) (1 atm)½ H⁺ (aq) (0.5 M) ½ ½ Fe²⁺ (10^-3 M)½ Fe⁰

a) Calcule o potencial de redução padrão do ferro (II), E⁰(Fe²⁺/Fe).

fem = E_dir –E_esq =
fem = E⁰_Fe2+/Fe – 0.0591/2 log(1/[Fe²⁺]) – { E⁰_H+/H – 0.0591/1 log[Ö(p_H2)/[H⁺]]} = –0.47
E⁰_Fe2+/Fe – 0.0591/2 log(1/(10^–3)) – { 0 – 0.0591/1 log[Ö(1)/(0.5)]} = –0.47
E⁰_Fe2+/Fe (25º C) = – 0.40 V

b) Identifique o cátodo e o ânodo da pilha.

Cátodo: eléctrodo da esquerda (H⁺/H₂)
Ânodo: o da direita (Fe²⁺/Fe)
Nota: a pilha está escrita de forma inversa (fem < 0).

c) Escreva as reacções parciais de eléctrodo e a reacção global da pilha.

Ânodo: Fe ® Fe²⁺ + 2e
Cátodo: H⁺ + e ® ½H₂
Global da pilha: Fe + 2H⁺ ® Fe²⁺ + H₂

Dados

N_A= 6.023´ 10²³ mol^-1R = 8.314 J. K^-1 mol^-1R_met(Fe) = 124 pm.
K_S(Mg(OH)₂;25ºC) = 7.1´ 10^-12
DHº_f (BaCO₃) = – 1219 kJ mol^-1
DHº_f (Ba²⁺) = – 537.6 kJ mol^-1
DHº_f (CO₃^2–) = – 677.14 kJ mol^-1
Eº (Fe²⁺/Fe) = – 0.440 V
Eº (Sn²⁺/Sn) = – 0.163 V
F = 96 480 C mol^-1

VIII/IX.5

Considere os seguintes compostos de carbono: metanol (CH₃OH), ácido fórmico (HCOOH) e formaldeído (H₂CO). O número de oxidação formal do carbono em cada um destes compostos será:
c	Igual, visto tratar-se do mesmo átomo.
c	C do metanol 2–, C do ácido fórmico 2+, C do formaldeído 0.
c	C do metanol 2–, C do ácido fórmico 0, C do formaldeído 0.
c	No metanol o C está numa forma mais oxidada e no ácido fórmico mais reduzida.
c	Não se define número de oxidação por serem compostos covalentes.

VIII/IX.6

Considere uma solução aquosa de ácido acético (CH₃COOH) 0.1 M. a 50 ºC?

i) Escreva a equação de dissociação do ác. acético e calcule a constante de acidez (constante de dissociação) a 25 ºC.

ii) Calcule a constante de acidez a 50 ºC e diga quais as aproximações usadas.

iii) Compare as constantes de acidez a 25 e 50 ºC e diga se a variação com a temperatura está de acordo com o Princípio de Le Chatelier.

iv) Calcule o pH da solução a 50 ºC.

NOTA: Nos cálculos não entre em conta com a contribuição do equilíbrio da água.

Dados

R = 8.314 J K^-1 mol^-1

Espécie	DGº_f (298) kJ/mol	DHº_f (298 K) kJ/mol
CH₃COOH(aq)	– 396.46	– 287.00
CH₃COO ^–_(aq)	– 369.31	– 238.55
H⁺_(aq)	0.00	0.00

VIII/IX.7

Na seguinte pilha a 25 ºC

Fe | Fe²⁺_(aq) (10^–1 M) || Cd²⁺_(aq) (10^–3 M) | Cd

o ânodo será o eléctrodo da direita ou da esquerda? Apresente os cálculos.

Eº (Fe²⁺/Fe) = – 0.44 V, Eº (Cd²⁺/Cd) = – 0.40 V

X.1

10.1. Sabendo que a resistividade a 300 K de três ligas cobre-níquel com composições 1.12, 2.16 e 3.32% (percentagem em peso de níquel) é, respectivamente, 3.2x10^-8 S^-1 m, 4.5x10^-8 S^-1 m e 5.8x10^-8 S^-1 m, calcule:

a) a condutividade do cobre puro a 300 K;

b) a resistividade residual de uma liga com 2% de níquel.

a) Regra de Nordheim logo, a variação com o teor de níquel deve ser linear.

De facto é aproximadamente linear, descrito por uma recta . Logo, de acordo com a Regra de Mathiessen e .

A condutividade do cobre puro é s = 1/r_T = 5.3x10⁷ S m^-1.

b) r_r (Cu+2%Ni) = 1.18x10^-6 S^-1 m x 0.02 = 2.4x10^-8 S^-1 m

X.2

10.6 Coloque por ordem crescente da largura da banda proibida os seguintes semicondutores silício (Si), arsenieto de gálio (GaAs) e selenieto de cádmio (CdSe). Justifique a resposta e classifique os semicondutores.

Trata-se em todos os casos de semicondutores intrínsecos porque o Si pertence ao grupo IV, o Ga ao IV-1 e o As ao IV+1, e o Cd ao IV-2 e o Se ao IV+2. Todos têm, em média, 4 electrões de valência para assegurar as ligações.

A largura da banda proibida depende da electronegatividade (e diferença de electronegatividade) dos elementos envolvidos na ligação. Podemos ver do seguinte modo: quanto mais electronegativos os elementos em ligação, mais localizadas serão estas e menos influem na energia das vizinhas. Assim, prevemos que o “gap” seja menor no Si (C_Si = 1.90), em seguida no GaAs (C_Ga = 1.81 C_As = 2.18) e maior no CdSe (C_Cd = 1.69 C_Se = 2.55) (essencialmente por causa da “alta electonegatividade” do Se que torna os electrões mais localizados).

X.3

10.7 Considere um semicondutor de silício (Si) contendo 0.1 % de alumínio (Al).

Esboce o respectivo diagrama de bandas.

Classifique o semicondutor.

Represente qualitativamente, num mesmo gráfico, o logaritmo das condutividade do semicondutor anterior e do silício puro, em função do inverso da temperatura.

O Al pertence ao grupo IV-1 logo a rede de Si fica deficiente em electrões junto ao alumínio que é uma impureza aceitante. É um semicondutor extrínseco tipo p.

Text Box: s (S/m) Text Box: Zona intrínseca Text Box: Zona extrínseca

X.4

Num semicondutor intrínseco à temperatura ambiente, a energia de Fermi será:
c	Exactamente no meio da banda proibida.
c	A energia para a qual o número de portadores positivos é idêntico ao número de portadores negativos.
c	Não se define energia de Fermi nos semicondutores intrínsecos porque corresponde a um nível proibido.
c	Correspondente ao último nível contendo electrões à temperatura ambiente.
c	Próximo do meio da banda proibida porque as massas efectivas dos portadores negativos e positivos são semelhantes.

X.5

Para o cálculo da densidade de portadores de carga, n ou p, é necessário saber g(E), a densidade de estados. Qual o significado físico desta função?
c	Dependência da temperatura do número de electrões por unidade volume, que é possível colocar num dado nível de energia E.
c	Dependência da temperatura do número de níveis permitidos para uma dada energia E.
c	Número de níveis permitidos (orbitais cristalinas) por unidade volume e de energia, para uma dada energia E.
c	Dispersão, em energia, das orbitais cristalinas por unidade volume, devido à formação dos portadores de carga (positivos e negativos).
c	Densidade de portadores de carga em torno do nível de Fermi para uma dada temperatura e energia.

X.6

Num semicondutor extrínseco, para muito baixas temperaturas a condutividade, s, aumenta com a temperatura (denominada zona extrínseca). Isto acontece porque:
c	Embora a mobilidade diminua, devido às ratoeiras, o número de portadores aumenta.
c	Nesta gama de temperatura os portadores de carga que se acumulam no nível de impureza aumentam a condutividade.
c	A facilidade em escapar às ratoeiras aumenta (aumenta a mobilidade) embora o número de portadores diminua (saem do nível de impureza).
c	O número de portadores aumenta devido à passagem de electrões da banda de valência para a de condução e a sua mobilidade também aumenta.
c	O número de portadores aumenta e a sua mobilidade também aumenta (aumenta a facilidade de escapar às ratoeiras).

X.7

Um condutor orgânico formado por moléculas sem heteroátomos (só com carbono e hidrogénio):
c	Será constituído por moléculas planares neutras, desordenadas, de massa molecular inferior a 1000
c	É constituído por moléculas planares com sistemas p deslocalizados, no estado neutro, separadas por catiões.
c	Pode obter-se por empilhamento ordenado de moléculas planares com sistemas p deslocalizados, oxidadas, com carga não inteira compensada pelos electrões livres.
c	Se for obtido por empilhamento ordenado de moléculas planares com sistemas p deslocalizados, oxidadas, com carga não inteira, sofre sempre uma transição para um estado supercondutor a baixa temperatura.
c	Se for obtido por empilhamento ordenado de moléculas planares com sistemas p deslocalizados, oxidadas, com carga não inteira, pode sofrer uma transição para um estado semicondutor a baixa temperatura.