|
IV.1 1.
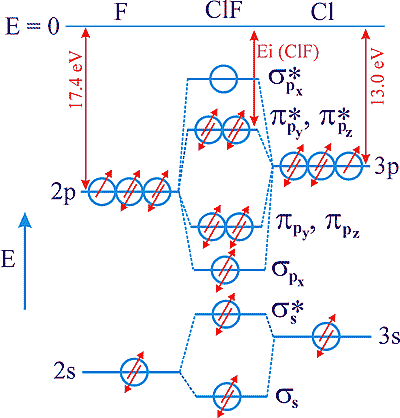
Desenhe o diagrama de energias para as orbitais moleculares da espécie diatómica
ClF indicando: i) as energias de ionização dos átomos constituintes e
da molécula, ii) os tipos de orbitais moleculares (s
, p , etc.) envolvidas,
iii) a ordem de ligação, iv) as propriedades magnéticas que prevê
para a molécula.
i) Ei indicadas no diagrama ii) Tipos de OM indicados no diagrama iii) OL = (8 – 6)/2 = 1 Cl–F iv) Diamagnética porque não tem electrões desemparelhados 2. Faça uma estimativa quantitativa do momento dipolar da molécula. momento dipolar ( mClF) = q ´ d = %CI/100 ´ e (carga do electrão) ´ dClFelectronegatividade (Cl) = 3.16 electronegatividade (F) = 3.98 diferença de electronegatividades = 0.82, a que corresponde uma percentagem de carácter iónico %CI= 15% (lida na Tabela Periódica) dClF = rcov(Cl) + rcov(F) = 99 pm + 72 pm = 171 ´ 10–12 mm ClF = 0.15 ´ 1.6 ´ 10–19 C ´ 171 ´ 10–12 m = 4.10 ´ 10–30 C m = 1.2 DIV.2 1. Desenhe o diagrama de energias das orbitais moleculares do monóxido de azoto (NO), identificando no mesmo diagrama as energias de ionização dos átomos constituintes e os tipos de orbitais moleculares (s, p, etc.) envolvidas. Determine a ordem de ligação no NO e preveja as propriedades magnéticas da molécula. 2. Utilizando os dados da Tabela Periódica faça uma estimativa do momento dipolar da molécula HF. 1. Molécula NO
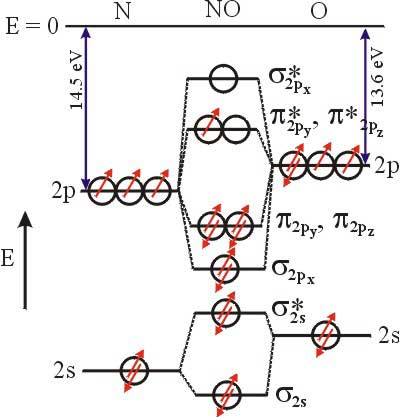
EI(N) = 14.5 eV
Configuração electrónica do azoto: 1s2
2s2 2p3
Diagrama de energia das orbitais moleculares Uma vez que a energia de ionização do N é maior que a energia de ionização do O as orbitais 2p do azoto têm menor energia. Representando apenas as orbitais de valência de ambos os átomos tem-se:
As orbitais atómicas sigma 1s não coalescem significativamente. Ficam, portanto, como orbitais não ligantes. NOTA: Nesta molécula as orbitais sigma 2p e pi 2p ligantes, são quase isoenergéticas (é a última molécula em que se observam os efeitos da inversão sigma-pi). Porém, tal como indicado nas aulas, não se espera que o aluno tenha em conta a inversão sigma-pi.
OL = (nº de electrões ligantes - nº de electrões
antiligantes)/2= (8 -3 )/2 = 2.5
2. Molécula HF momento dipolar (mHF) = q x d = %CI/100 x e (carga do electrão) x dHF
electronegatividade do H=2.2
diferença de electronegatividades
= 1.78, a que corresponde uma percentagem de carácter iónico
%CI= 55% (lido
na Tabela Periódica)
mHF = 0.55 x 1.6x10-19 C x 102 x10-12 m = 8.976 x10-30 C m = 2.7 D IV.3 1. Desenhe o diagrama de orbitais moleculares do ião N2+, identificando no mesmo diagrama as energias de ionização dos átomos constituintes e os tipos de orbitais moleculares (s, p, etc.) envolvidas. Determine a ordem de ligação nesta espécie e preveja as propriedades magnéticas da molécula. 2.
Utilizando os dados da Tabela Periódica faça uma estimativa
do momento dipolar da molécula LiH.
Dados e constantes de conversão:
|