Biomédica, MEFT

Exercícios resolvidos

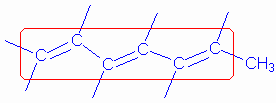
1.  Calcule o comprimento de onda correspondente à transição 0-0 da banda de absorção de menor energia no UV-Vis do 1,3,5-heptatrieno (CH2CHCHCHCHCHCH3) previsto pelo modelo da partícula na caixa. Admita dC-C= 141 pm.

Esta molécula apresenta 6 electrões π deslocalizados, logo estão preenchidas as orbitais com n=1, n=2 e n=3. O modelo prevê que a transição de menor energia se dê entre as orbitais com n=3 e n=4.  O comprimento da caixa corresponde a 6 dC-C.

Comprimento da caixa, L = 6 x dC-C= 6 x 141 pm = 846 pm = 8.46 x 10–10 m
Número de electrões π na caixa (1 por cada átomo de carbono na cadeia) = 6

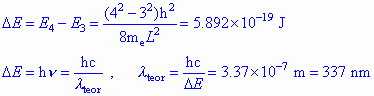
2. No contexto do modelo da partícula na caixa linear de potencial quais os números quânticos que caracterizam um electrão num dado nível?

n (número quântico principal), e ms (número quântico magnético de spin)

3. Considere a molécula de 1,3-butadieno [CH2CHCHCH2]. Explique como o modelo da partícula numa caixa unidimensional de potencial prevê comprimentos de ligação C1-C2 mais curtos que o do ligação C2-C3. Calcule o comprimento de onda da transição de menor energia no UV-Vis previsto por este modelo e compare com o valor experimental (238 nm). 

Esta molécula apresenta quatro electrões  π deslocalizados, logo estão preenchidas as orbitais com n=1 e n=2.
As funções de onda que descrevem estes electrões são representadas na figura,  onde  se representa igualmente o quadrado das funções de onda e a sua soma. Como vemos, a densidade electrónica entre C2 e C3 é menor do que entre C1 e C2, que é idêntica à densidade electrónica entre C3 e C4 (isto devido ao nodo que a função de onda n=2 apresenta no centro da caixa). Logo a distância internuclear C2 e C3 é maior.

Este modelo prevê que a transição electrónica de menor energia se dê entre as orbitais com n=2 e n=3.  O comprimento da caixa corresponde a 4 dC-C

ΔE = E3-E2
L = 4x 1.21x10-10   m =  4.84 x10-10   m
ΔE = h2 (32-22) /  8 m (4.84x10-10)2
ΔE = h ν = h c / λ
λ = h c / ΔE
λ=  2.1x10-7 m =  210  nm

A surpreendente  pequena diferença* entre o comprimento de onda de absorção do butadieno previsto pelo modelo e o valor experimental é devida às aproximações do modelo:

* maior quanto maior for o número de electrões π da molécula considerada.

4. Explique quantitativamente a seguinte afirmação: O neon tem uma energia de ionização elevada e uma electroafinidade baixa.

A energia de ionização e a electroafinidade são proporcionais à razão (Zef /n)2  para o electrão em causa.

Configuração electrónica do Ne: (1s2)(2s2 2p6)                         Configuração electrónica do Ne-: (1s2 )(2s2 2p6)(3s1)

EI(Ne) é proporcional a  (Zef /n)2(2p, Ne)
EA(Ne) é proporcional a  (Zef /n)2(3s, Ne-)
 
 Zef (2p, Ne) = 10 - (7x0.35 + 2x0.85) = 5.85
Zef (3s, Ne-) = 10 - (8x0.85 + 2x1) = 1.2

(Zef /n)2 (2p, Ne) = (5.85/2)2= 8.56
(Zef /n)2 3s, Ne-) = (1.2/3)2= 0.16

A energia de ionização do Ne é elevada porque a razão (Zef /n)2  para o electrão removido é muito elevada (comparar com os valores obtidos para o azoto e oxigénio no exemplo seguinte); a electroafinidade é baixa porque também é baixa a razão (Zef /n)2  para o electrão fornecido ao Ne para formar a espécie mononegativa. 

5. Explique os valores experimentais das energias de ionização do azoto (N) e do oxigénio (O) que encontra na Tabela Periódica.

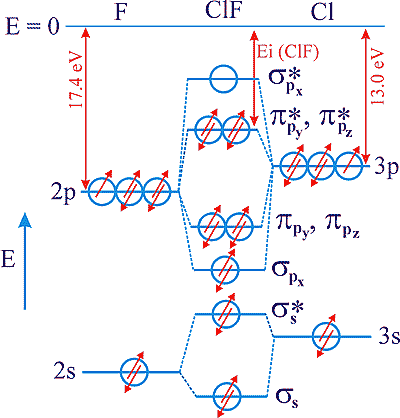
A energia de ionização é proporcional à razão (Zef /n)2  para o electrão em causa.
EI(N) = 14.5 eV
EI(O) = 13.6 eV
Configuração electrónica do azoto: (1s2)(2s22p3)
Zef (2p, N) = 7 - (4x0.35 + 2x0.85) = 3.9 Configuração electrónica do oxigénio: (1s2)(2s22p4)
Zef (2p, O) = 8 - (5x0.35 + 2x0.85) = 4.55
(Zef /n)2(2p, N) = (3.9/2)2= 3.8
(Zef /n)2(2p, O) = 5.2

A energia de ionização do oxigénio deveria ser superior à energia de ionização do azoto, uma vez que a razão (Zef /n)2  é maior para o electrão 2p do oxigénio. Experimentalmente verifica-se que a energia de ionização do azoto é superior porque as regras de Slater não contemplam o grau de preenchimento das orbitais, isto é, não consideram a repulsão interelectrónica. No azoto o electrão  é removido de uma orbital semipreenchida enquanto no oxigénio o electrão é removido de uma orbital completamente preenchida.

6. Considere espécie diatómica ClF.
    a) Desenhe o diagrama de energias para as orbitais moleculares do ClF,  indicando as energias de ionização dos átomos constituintes e da molécula,  os tipos de orbitais moleculares (σ ou π, envolvidas. Calcule  a ordem de ligação e as propriedades magnéticas que prevê para a molécula.
    b) Faça uma estimativa do momento dipolar desta molécula.

a)

EI(F) = 17.4 eV
EI(Cl) = 13.0 eV

Configuração electrónica de valênciado flúor: 2s2 2p5
Configuração electrónica do cloro:  3s2 3p5

Uma vez que a energia de ionização do F é maior que a energia de ionização do Cl as orbitais 2p do flúor têm menor energia. Representando apenas as orbitais de valência de ambos os átomos tem-se:






A molécula  é diamagnética uma vez que não apresenta electrões desemparelhados.

OL (ClF)=  (8-6)/2 = 1
 
b)
Molécula ClF

electronegatividade:  χ F =3.98   e   χ Cl =3.16

Δχ = 0.82 a que corresponde (lido na Tabela Periódica) uma percentagem de carácter iónico  %CI= 15%
 

momento dipolar
μLiF = %CI/100 x e (carga do electrão) x dClF

dClF = rcov(Cl) + rcov (F) = (99 + 72) x10-12 m =  171 x10-12 m

μClF = 0.15 x 1.6x10-19 C x 171 x10-12m = 4.10 x10-30 C.m = 1.2 D


6. a) Desenhe o diagrama de orbitais moleculares do monóxido de azoto (NO), identificando no mesmo diagrama as energias de ionização dos átomos constituintes e os tipos de orbitais moleculares (sigma, pi, etc.) envolvidas. Determine a ordem de ligação no NO e preveja as propriedades magnéticas da molécula.
    b) Utilizando os dados da Tabela Periódica faça uma estimativa do momento dipolar da molécula HF.

EI(N) = 14.5 eV
EI(O) = 13.6 eV

Configuração electrónica do azoto: 1s22s2 2p3
Configuração electrónica do oxigénio: 1s2 2s2 2p4

Uma vez que a energia de ionização do N é maior que a energia de ionização do O as orbitais 2p do azoto têm menor energia. Representando apenas as orbitais de valência de ambos os átomos tem-se:


OL = (nº de electrões ligantes -  nº de electrões antiligantes)/2= (8 -3 )/2 = 2.5
A molécula é paramagnética.

b) 

electronegatividade: χH=2.2  e χF=3.98

Δχ = 1.78 a que corresponde (lido na Tabela Periódica) uma percentagem de carácter iónico  %CI= 55%
 
momento dipolar
μHF = %CI/100 x e (carga do electrão) x dHF
dHF = rcov(H) + rcov (F) = (30 + 72) x10-12 m =  102 x10-12 m
μHF = 0.55 x 1.6x10-19 C x 102 x10-12m = 8.976 x10-30 C.m = 2.7 D 



Biomédica, MEFT